Quantas vezes um pedaço de papel A4 pode ser dobrado?
É um equívoco comum que um pedaço de papel A4 só possa ser dobrado ao meio aproximadamente 7 vezes, no máximo 8 vezes. Os caras do Mythbusters (Caçadores de Mitos) pensaram que pegariam um pedaço de papel A4 e eles dobrariam o papel mais de oito vezes. Eles realmente dobraram o pedaço de papel 11 vezes.

Após essa façanha, a explicação deles para a impossibilidade de realizar uma décima segunda dobra no papel A4 foi que ela teria produzido algo parecido com um semicírculo e não com uma dobra real.
Uma estudante chamada Brittany Gallivan conseguiu dobrar com sucesso um pedaço extremamente longo de papel higiênico pela metade doze vezes. Mais tarde, os alunos da escola St. Marks, em Southborough, juntamente com o professor James Tanton, afirmaram que conseguiram dobrar um pedaço de papel higiênico ainda mais longo um total de treze vezes, quebrando o recorde anterior estabelecido por Gallivan.
Mas, de acordo com Gallavan, ela alegou que tanto os estudantes de Mythbusters quanto os de Southborough haviam “infringido as regras”. Brittany explicou em um comunicado à imprensa que Mythbusters e os estudantes de St. Marks tinham admitidamente usado papel A4 que precisava ser colado, em vez de a única folha exigida por este desafio de dobragem de papel.
Quando Gallavan fez doze dobras, ela o apoiou com um livro intitulado “Como dobrar papéis pela metade doze vezes: um desafio impossível resolvido e explicado”, que foi o que inspirou os estudantes de Southborough a quebrar seu recorde. Em seu livro, ela observou exatamente como ela era capaz de realizar esse truque e também o apoiou com algumas equações matemáticas que explicavam com precisão sua vitória e as limitações que esse desafio apresentava.
Aqui vem a matemática!
Quando ela foi originalmente apresentada a esse problema por um de seus professores de matemática do ensino médio, para alcançar uma dúzia de vincos, ela criou uma equação que tratava de dobrar o papel A4 pela metade da maneira tradicional, de cima para baixo e de um lado para o outro. Onde a largura resulta da espessura do material e do número de dobras.
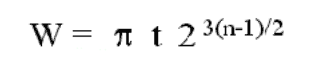
Ela então criou uma segunda equação em que acreditava que poderia vencer esse desafio dobrando o papel ao meio longitudinalmente e continuando a dobrá-lo dessa maneira. Aqui o comprimento foi derivado da espessura do papel A4 e do número de dobras.
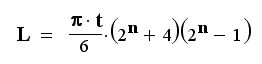
Sua conclusão foi que, a cada dobra longitudinal, seriam necessários aproximadamente quatro vezes mais papel para chegar a uma dúzia.
O que esse matemático finalmente conseguiu provar com suas equações é que quanto menor e mais grosso o pedaço de papel, A4 menos vezes você pode dobrá-lo e vice-versa.
À medida que continuamos a dobrar, a metragem quadrada menor do papel não permite que a espessura das dobras continue, o que faz sentido lógico.
A conclusão é que, à medida que a altura das dobras continua a aumentar, à medida que a quantidade de papel também aumenta, a espessura aumenta exponencialmente.
Em outras palavras, para um número de dobras, você terá 2^n pedaços de papel de espessura. Isso adiciona rapidamente. 3 dobras: 2 x 2 x 2 = 8 pedaços de papel de espessura.
Quando você alcança 7, está com 2^ 7 ou 2 x 2 x 2 x 2 x 2 x 2 x 2 = 128 pedaços de espessura. Não foi possível fazer a 8ª dobra, porque 256 pedaços de papel A4 são como tentar dobrar um pedaço de madeira.
O papel A4 Fica exponencialmente grosso
A espessura cresce tão exponencialmente rápido; de fato, segundo outro matemático, essas quantidades podem ser surpreendentes, estendendo os limites do universo conhecido. Suas figuras mostram que conforme a pilha dobrada cresce…
- Com 23 dobras, você alcançará um quilômetro ou 3.280 pés
- 30 dobras o levarão ao espaço sideral a 100 quilômetros ou pouco mais de 62 milhas
- Mais de 40 vão pousar na lua
- Um pouco mais de 50 leva você ao sol
- Mais de 80 dobras estão próximas da espessura da galáxia de Andrômeda, estimada em 141.000 anos-luz de largura
- Quase 90 dobras e será maior que o superaglomerado de Virgem, com cerca de 130 milhões de anos-luz de comprimento
- Finalmente, com 103 dobras, você agora está fora do universo observável, estimado em 92 bilhões de anos-luz de diâmetro.
Embora esses matemáticos e estudantes possam ver claramente os números para realizar ainda mais dobras, até os confins do universo e vice-versa, mas a que preço?
Até que ponto, literalmente, estamos dispostos a ser o campeão de dobrar papel? Quanto tempo estamos dispostos a gastar? Quantas árvores devem morrer para realizar nossos sonhos? Quem será nosso próximo herói de papel dobrável?
No caso de Brittany, o custo para seu rolo extra-longo de papel higiênico era de $85 (Oitenta e cinco doláres) e o comprimento era de quase 4.000 pés, como mencionado anteriormente, e 13.000 pés para os estudantes de Southborough.
Brittany levou sete horas para chegar à décima primeira dobra e tirar sua foto, posteriormente, fazer a décima segunda e última dobra. Tudo isso era simplesmente obter algum crédito extra em sua aula de matemática do ensino médio.
Esses profissionais de dobragem de papel continuam falando sobre “quebrar um recorde”, mas é realmente um recorde mundial se nem é reconhecido pelo Guinness?
De acordo com Tanton, professor de St. Marks, as pessoas do Guinness Book of World Records nem sequer têm uma categoria para pasta de papel e não acompanham esses tipos de registros, o que é uma pena.
E quanto à alegação de Gallivan de que tanto a equipe dos Mythbusters quanto os estudantes não seguiram as regras de ser um pedaço contínuo de papel, quem as criou em primeiro lugar? Foi a professora dela? Acho que você terá que comprar o livro dela para descobrir.
No que diz respeito à notoriedade, obviamente Gallivan obteve bastante reconhecimento on-line por sua conquista e ainda está vendendo cópias de seu livro.
Sua equação também foi mencionada na série principal da CBS, “Numb3rs”, onde um jovem matemático ajuda seu irmão mais velho a resolver crimes para o FBI usando várias equações.
E em conclusão
Hoje, dissipamos o mito de que o papel A4 só pode ser dobrado ao meio 7 ou 8 vezes. Muitas pessoas e grupos tentaram fazer as dobras de papel A4.
Uns conseguiram, no entanto – Mythbusters, Bretanha e os estudantes de Southborough – conseguiram até 13 dobras. Também aprendemos uma nova maneira de ficar famoso: dobre um único pedaço de papel pela metade 14 vezes.





